本問題では「数学の基礎・基礎解析」のうち「微分積分」について学びます。
本問題の解説はYouTube動画でもご覧いただけます。
【解説動画】 第1回Python3データ分析模擬試験 第11問
※当解説動画シリーズはPythonエンジニア育成推進協会に認定された「Python 3 エンジニア認定データ分析試験」の参考教材です。
【補足】
今回はデータ分析の前提として、基礎的な「数学」の解説となります。
問題文や選択肢に「右辺～」と表現がありますが、Python データ分析の本質的な考え方として右辺や左辺にかかわらず、関数に微分積分を行うことです。
誤解がないようにご留意頂けますこと、よろしくお願いいたします。
問題
右辺が6x^2（6掛けるxの二乗）で表現される関数をf(x)とする。微分積分に関する以下の記述のうち誤っているものはどれか。
① 関数f(x)を微分すると、右辺は12xとなる。
② 関数f(x)を積分すると、右辺は3x^3となる。
③ 積分の範囲が決められていないものを不定積分、範囲が決められているものを定積分という。
④ 微分は傾き、積分は面積と捉えることができる。データ分析や機械学習において、関数の傾きが0となる点は有益な情報として利用される。
⑤ 多変数関数の微分を偏微分という。偏微分の場合、変数が複数あるので、どの変数で微分したのかを示すことが必要となる。
解説
正解は選択肢②です。以下、解説します。
選択肢①
元の関数ｆ(x)=6x^2を公式に当てはめて微分すると、結果は12xとなります。
選択肢②
選択肢②は、誤りです。
元の関数ｆ(x)=6x^2を公式に当てはめて積分すると、結果は2x^3+C（Cは積分定数）となります。
選択肢③
選択肢③は、正しい肢です。
定積分と不定積分の定義が述べられています。
選択肢④
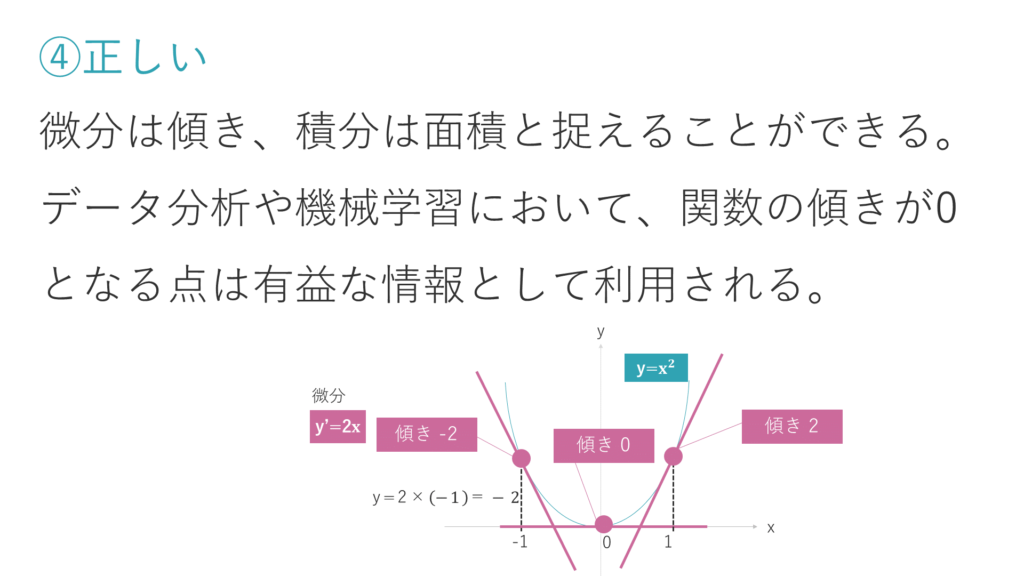
選択肢④は、正しい肢です。
右図のような「y＝x^2」というグラフがあります。y＝x^2を微分すると、2xになります。この2xはグラフの傾きを表します。
例えば、y＝x^2のxがｰ1なら傾き（2x）は2×(-1)で-2、xが1なら傾きは2×1で2、xが0なら傾き2×0で0です。
このことは、データ分析や機械学習において、以下のように利用されます。
データ分析での利用方法
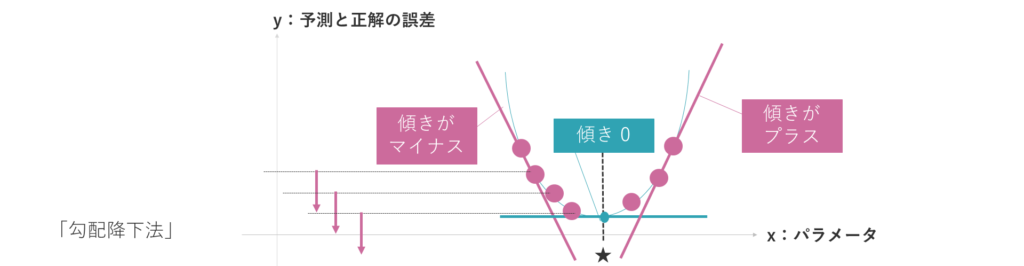
例えば右図のような、y＝x^2の曲線があります。横軸がパラメータ、縦軸が予測と正解の誤差だとします。
このグラフにおいて、誤差を可能な限り小さくしたいとしましょう。そこで誤差を最小にできるような最適なパラメータを探していきます。
例えば傾きがマイナスの値である場合、これが意味するものは、パラメータを、右方向に調整すると、もっと誤差を縮められるということです。
逆に、傾きがプラスの値の時は、これ以上パラメータを右方向に動かすともっと誤差が大きくなってしまう、だから左方向に調整したほうがいい、ということです。
このように、傾きの値を見ながらパラメータを調整していくことで、最終的には傾きがゼロの点、つまり正解と予測の誤差がもっとも少ない最適なパラメータが見つかります。
これが「関数の傾きがゼロの点は有益である」ということの意味です。
このような関数の傾きに着目して最適なパラメータを探す方法を「勾配降下法」といいます。
選択肢⑤
選択肢⑤は、正しい肢です。
例えば右図にあるような、xとyの2つの変数からなる多変数関数では、xでもyでも微分することができます。
いずれの場合も、どの変数で微分するのかが計算には必要です。
第1回Python3データ分析模擬試験第11問の解説は以上です。