第1回Python3データ分析模擬試験【第09問】解説

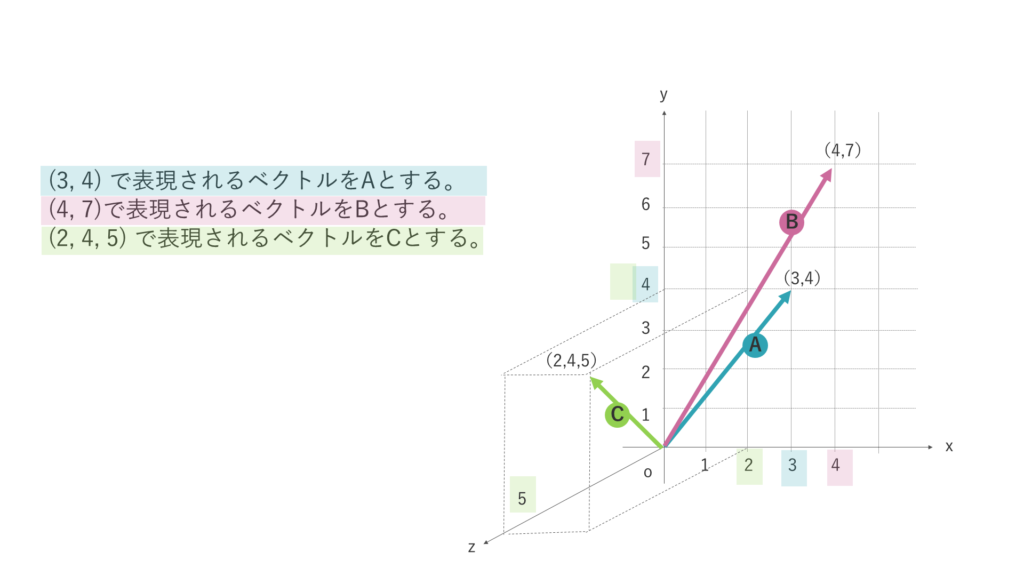
問題文のベクトル（(3, 4) で表現されるベクトルをAとする。(4, 7)で表現されるベクトルをBとする。(2, 4, 5) で表現されるベクトルをCとする）を図示すると、右図のようなものであることが確認できます。

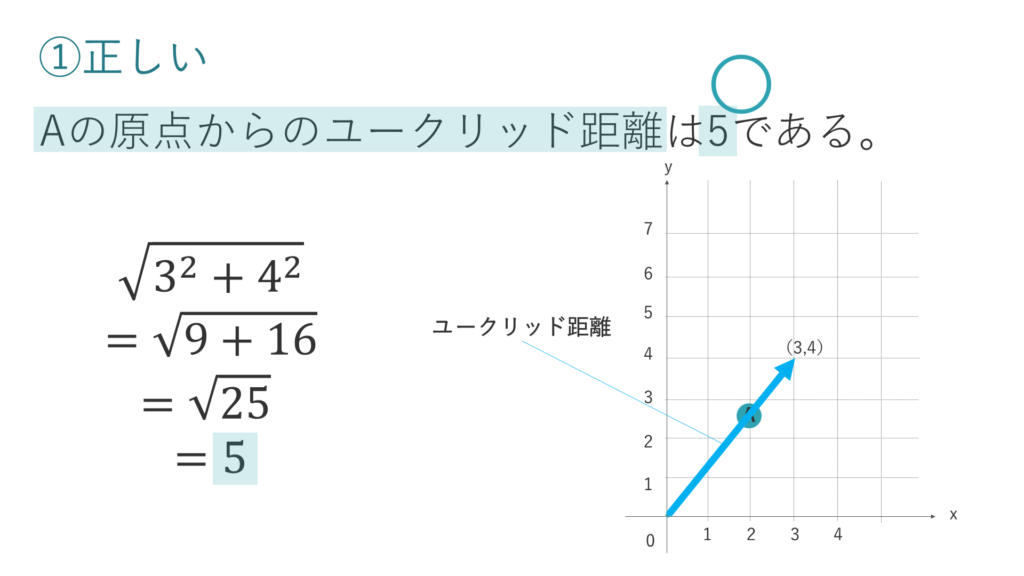
選択肢①は、正しい肢です。

Aベクトルの原点からのユークリッド距離は、原点から終点までの直線距離です。

ユークリッド距離の公式に当てはめて計算すると、答えは「5」となります。

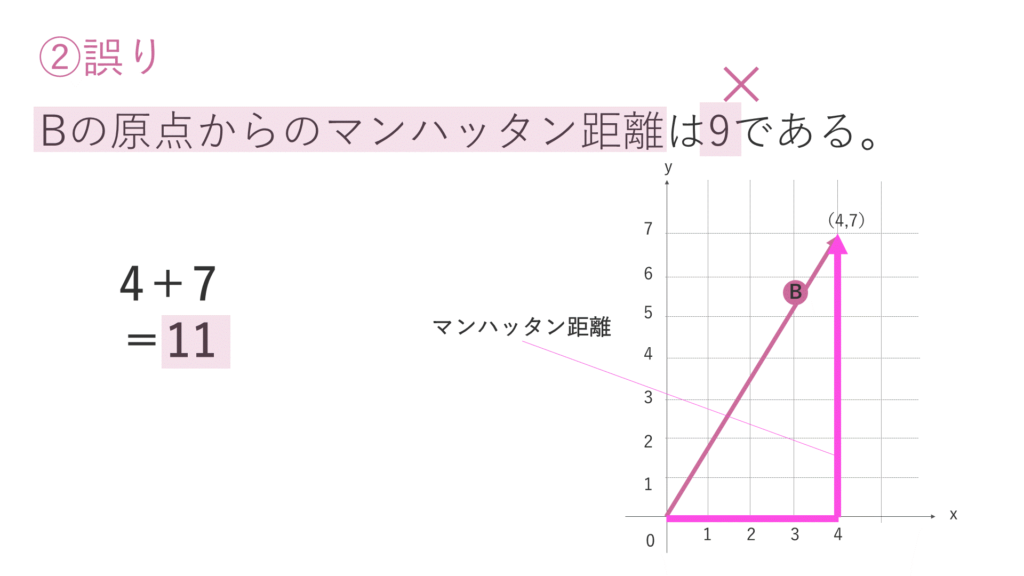
選択肢②は、誤りの肢です。

Bベクトルの原点からのマンハッタン距離は、原点から座標軸に沿って終点に至るまでの距離です。

マンハッタン距離の公式に当てはめて計算すると、答えは「11」となります。

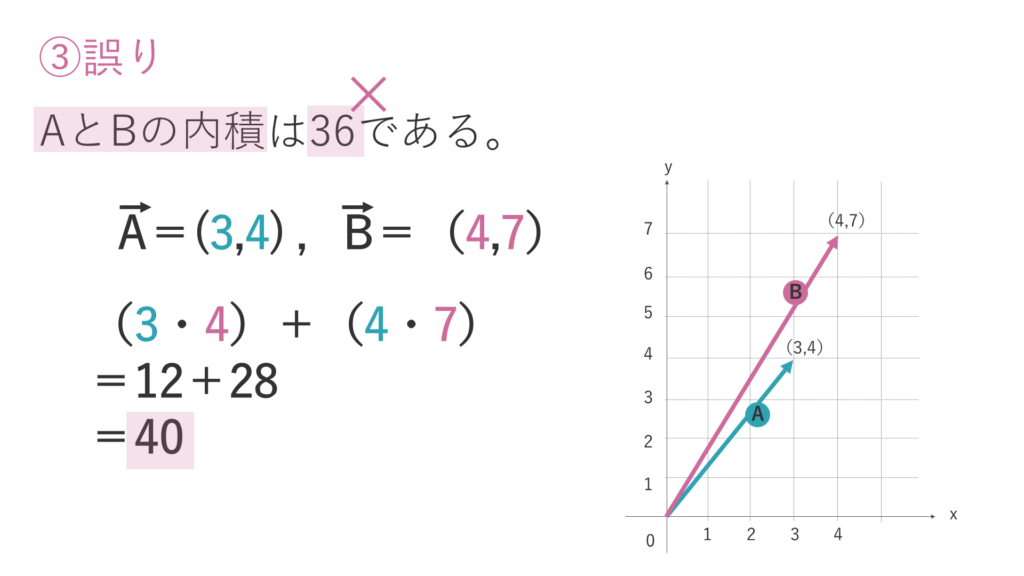
選択肢③は、誤りです。

AベクトルとBベクトルの内積の計算をすると、答えは「40」となります。

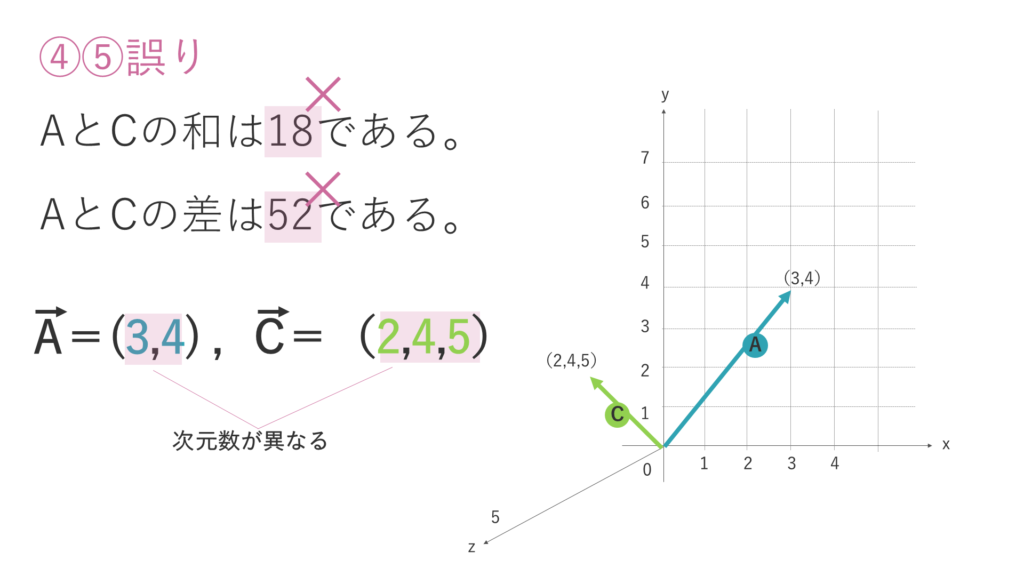
選択肢④と⑤は、いずれも誤りです。

Aベクトルは2次元の平面ベクトル、Cベクトルは3次元の空間ベクトルであり、次元数・要素数が異なります。

次元数の異なるベクトルの足し算・引き算はできません。