本問題では「数学の基礎・線形代数」のうち「行列、正方行列・単位行列、行列の計算」について学びます。
本問題の解説はYouTube動画でもご覧いただけます。
【解説動画】 第1回Python3データ分析模擬試験 第10問
※当解説動画シリーズはPythonエンジニア育成推進協会に認定された「Python 3 エンジニア認定データ分析試験」の参考教材です。
問題
行列に関する次の記述のうち誤っているものはどれか。
① 行と列のサイズが同じ行列を特に正方行列と呼び、正方行列のうち、対角成分がすべて0で、残りの要素が1の行列を単位行列と呼ぶ。
② ベクトルと同じように要素同士の足し算と引き算で、行列の足し算と引き算を定義することができるが、2つの行列の行数と列数が合っている必要がある。
③ 行列の列の数とベクトルのサイズが同じ場合は、これらの掛け算を定義することができ、結果は、元の行列の行数と同じサイズのベクトルになる。
④ 行列同士の掛け算は行列となる。数値の掛け算は順番を入れ替えても同じ結果となるが、行列の掛け算は順番を入れ替えると同じ結果になるとは限らない。
⑤ m×sの行列にs×nの行列を賭けると、m×nの行列になる。これを逆に考えると、データ分析や機械学習において、説明変数の次元数を削減することができる。
解説
正解は選択肢①です。以下、解説します。
選択肢①
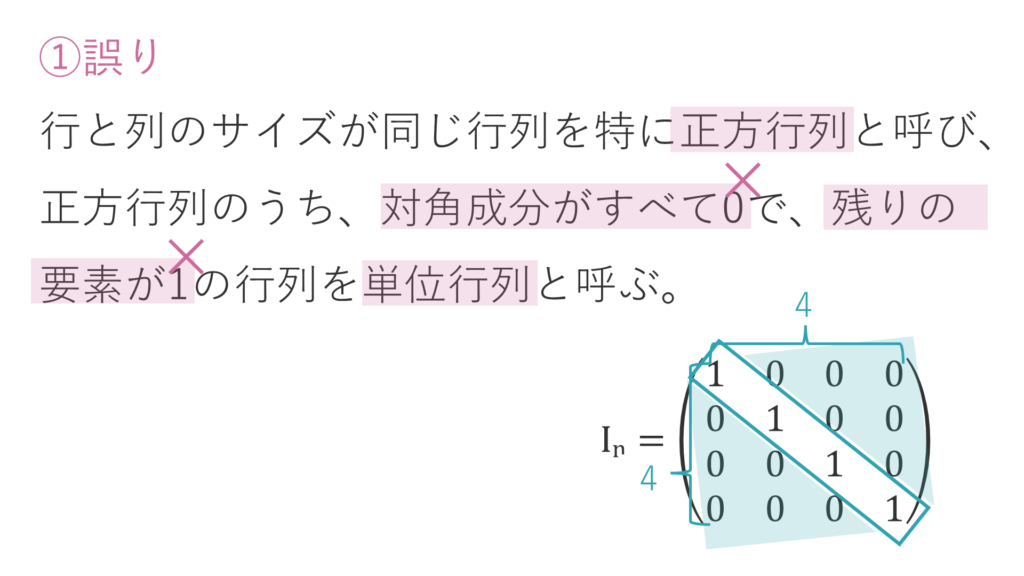
選択肢①は、誤りです。
例えば右図右下にある4×4行列のように、行と列の数が同じものが「正方行列」です。
単位行列とは、正方行列のうち対角成分がすべて1であり、かつ、残りの要素がすべて0の行列です。
選択肢②
選択肢②は、正しい肢です。
例えば右図の行列A、行列Bは、どちらも2×２行列です。
そのため要素同士で足し算、また引き算を行うことができます。
選択肢③
選択肢③は、正しい肢です。
行列Aは3×2行列で2列、ベクトルxの要素数が2なので、掛け算ができます。結果は要素数３のベクトルとなります。
選択肢④
選択肢④は、正しい肢です。
行列の掛け算は順番を入れ替えると、原則として同じ結果にはなりません。
例えば右図のように、同じ2×２行列の行列Aと行列Bを、順序を入れ替えて2度掛け算すると、両者の結果は異なります。
ただし、例外的に正方行列の場合、単位行列との掛け算は順番を入れ替えても同じ結果となります。
選択肢⑤
選択肢⑤は、正しい肢です。
問題文前半は行列の分解について、後半は次元削減について述べられています。
行列の分解
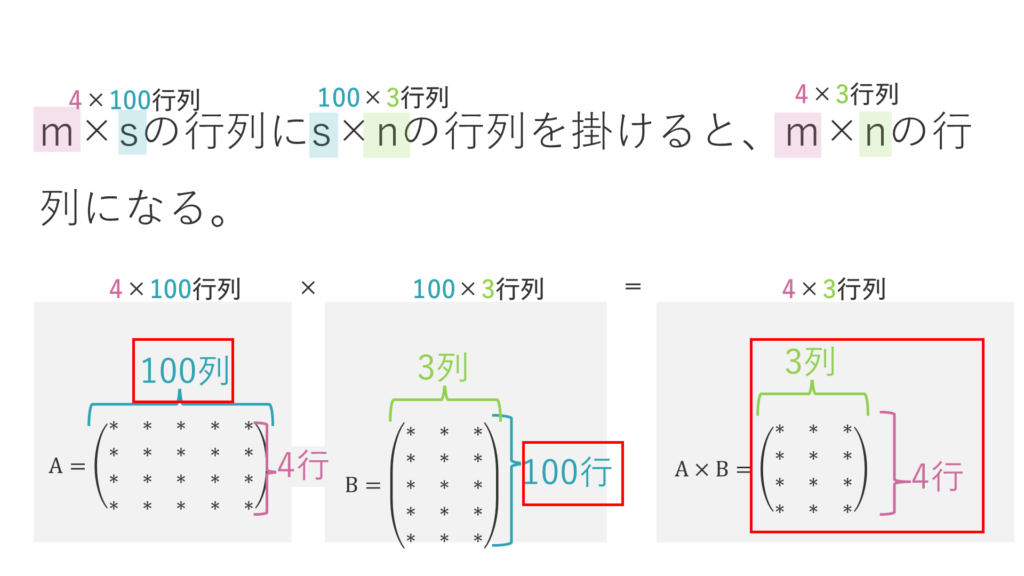
行列同士の掛け算は、（右図でいうと）行列Aの列数と行列Bの行数が同じであれば、可能です。
そこで、例えば右図のように4×100行列と、100×3行列の掛け算をすると、結果は、行列Aの行数かつ行列Bの列数からなる行列となります。
つまりかなり複雑な計算をしたにもかかわらず、結果はシンプルな4×3行列です。
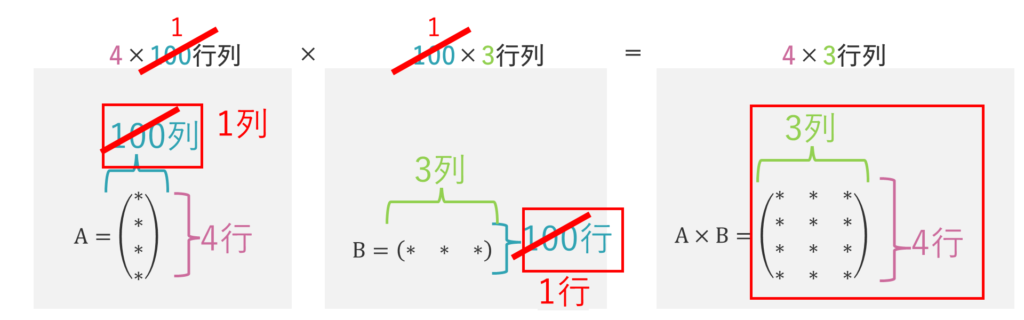
結果のほうから掛け算の式を考えてみると、4×3行列（結果）は、4×100行列と、100×3行列に分解できるともいえます。
そして4×3行列をつくるためには、実は、（右図のように）4×1行列、1×3行列の掛け算でも可能である、行列Aと行列Bは、もっと簡単に考えることができるということです。
次元削減
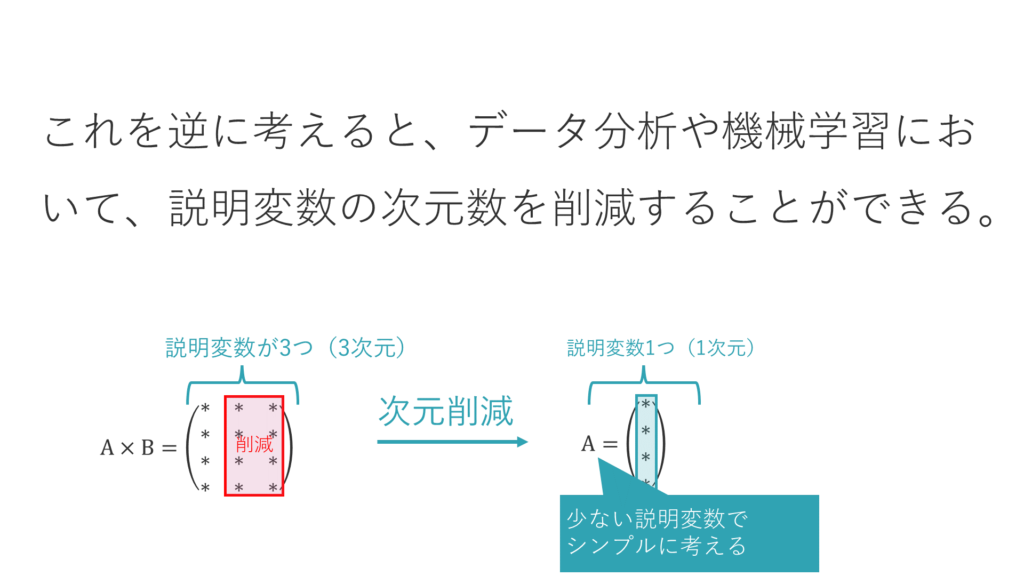
こうした考え方は、データ分析や機械学習で、説明変数の次元数を削減することに通じます。
つまり結果に与える影響の少ない説明変数を削ることで、サンプルをシンプルに考えらるようになるということです。
第1回Python3データ分析模擬試験第10問の解説は以上です。